Description
Flux control efficiencies express the control of respiration by a metabolic control variable, X, as a fractional change of flux from YX to ZX, normalized for ZX. ZX is the reference state with high (stimulated or un-inhibited) flux; YX is the background state at low flux, upon which X acts.
- jZ-Y = (ZX-YX)/ZX = 1-YX/ZX
Complementary to the concept of flux control ratios and analogous to elasticities of metabolic control analysis, the flux control efficiency of X upon background YX is expressed as the change of flux from YX to ZX normalized for the reference state ZX. » MiPNet article
Abbreviation: jZ-Y
Reference: Gnaiger 2020 BEC MitoPathways
Flux control efficiency: normalization of mitochondrial respiration
| Gnaiger E (2020) Flux control efficiency: normalization of mitochondrial respiration. Mitochondr Physiol Network 2016-03-20; updated 2020-11-10. |
» Gnaiger 2020 BEC MitoPathways
Abstract: The flux control efficiency, jZ-Y, and flux control ratio, FCR, are internal normalizations, expressing respiratory flux in a given state relative to respiratory flux in a reference state. Whereas FCRs express various respiratory states relative to a common refrence state, jZ-Y express the control of respiration in a single step caused by a specific metabolic control variable X. The concept of the flux control efficiency presents a generalized framework for assessing the effect of an experimental variable on flux and defines specific expressions, such as the biochemical coupling efficiency.
• O2k-Network Lab: AT Innsbruck Gnaiger E
Metabolic control variable and respiratory state
- A metabolic control variable X is either added (stimulation, activation) or removed (reversal of inhibition) to yield a high flux Z in the reference state, compared to flux Y in the background state. X denotes the metabolic control variable; Y and Z are the respiratory states, whereas Y and Z denote the corresponding respiratory fluxes. jZ-Y in step analysis relates to the change of flux caused by the variable X. The FCR in state analysis compares fluxes in a variety of respiratory states which may be separated by single or multiple variables, i.e. separated by several coupling and pathway control states.
- If inhibitors are experimentally added rather than removed (-X); then YX is the background rate in the presence of the inhibitor.
- X: Metabolic control variable acting on YX in the background state, to yield rate ZX in the reference state. X stimulates or un-inhibits YX from low flux to ZX at high flux.
- YX: The rate in the background state Y is the non-activated or inhibited respiratory rate (low) in relation to the high rate ZX in the reference state Z. A metabolic control variable, X, acts on YX (substrate, activator) or is removed from Y (inhibitor) to yield ZX. The X-specific (in contrast to general) flux control ratio is Y/Z.
- ZX: The rate in the reference state Z, stimulated or un-inhibited by a metabolic control variable, X, with high rate in relation to rate YX in the background state Y.
- If inhibitors are experimentally added rather than removed (-X); then YX is the background rate in the presence of the inhibitor.
Pathway control efficiency
- Pathway control efficiencies express the relative change of oxygen flux in response to a transition of (1) CHNO-fuel substrates or (2) inhibitors of enzyme steps in the pathway, in a defined coupling state.
- » NS-N pathway control efficiency
Coupling-control efficiency
- Coupling-control efficiencies are determined in an ET-pathway competent state. The terms coupling efficiency and coupling-control efficiency are used synonymously.
mt-Preparations


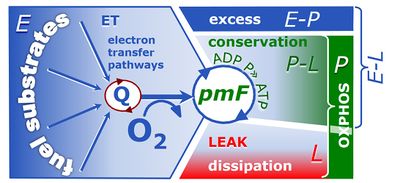
 In mitochondrial preparations, there are three well-defined coupling states of respiration, L, P, E (LEAK respiration, OXPHOS, Electron transfer pathway).
In mitochondrial preparations, there are three well-defined coupling states of respiration, L, P, E (LEAK respiration, OXPHOS, Electron transfer pathway).
- 1. If the metabolic control variable, X, is an uncoupler, the reference rate ZX is E. Then two background states Y, of coupling control are possible: The uncoupler may act on L or P in mt-preparations. The corresponding flux control efficiencies are:
- E-L coupling efficiency, jE-L = (E-L)/E = 1-L/E.
- E-P control efficiency, jE-P = (E-P)/E = 1-P/E.
- 1. If the metabolic control variable, X, is an uncoupler, the reference rate ZX is E. Then two background states Y, of coupling control are possible: The uncoupler may act on L or P in mt-preparations. The corresponding flux control efficiencies are:
- 2. If the metabolic control variable is stimulation by ADP, D, or release of an inhibitor of phosphorylation of ADP to ATP (DT-phosphorylation; e.g. -Omy), the reference rate Z is P at saturating concentrations of ADP. The background rate Y is L, and the corresponding flux control efficiency is:
- P-L control efficiency, jP-L = (P-L)/P = 1-L/P, related to the RCR.
- 2. If the metabolic control variable is stimulation by ADP, D, or release of an inhibitor of phosphorylation of ADP to ATP (DT-phosphorylation; e.g. -Omy), the reference rate Z is P at saturating concentrations of ADP. The background rate Y is L, and the corresponding flux control efficiency is:
- 3. If the background rate Y is L, the metablic control variable from L to P is ADP-saturated ATP turnover or release of an inhibitor of phosphorylation of ADP to ATP, and the reference rate Z is E, the coupling control ratio is expressed as the net P/E control ratio (compare 1 and 2):
- (P-L)/E
- 3. If the background rate Y is L, the metablic control variable from L to P is ADP-saturated ATP turnover or release of an inhibitor of phosphorylation of ADP to ATP, and the reference rate Z is E, the coupling control ratio is expressed as the net P/E control ratio (compare 1 and 2):
Living cells


 L(Omy) and E can be induced in living cells, but rate P cannot. However, the ROUTINE rate of respiration R can be measured in living cells.
L(Omy) and E can be induced in living cells, but rate P cannot. However, the ROUTINE rate of respiration R can be measured in living cells.
- 1. If the metabolic control variable X is an uncoupler, the reference rate Z is E. Then two background states, Y of coupling control are possible: The uncoupler may act on the LEAK respiration or ROUTINE state in living cells. The corresponding coupling control efficiencies are:
- E-L coupling efficiency, jE-L = (E-L)/E = 1-L/E.
- E-R control efficiency, jE-R = (E-R)/E = 1-R/E.
- 1. If the metabolic control variable X is an uncoupler, the reference rate Z is E. Then two background states, Y of coupling control are possible: The uncoupler may act on the LEAK respiration or ROUTINE state in living cells. The corresponding coupling control efficiencies are:
- 2. If the metabolic control variable is stimulation by ATP turnover or release of an inhibitor of phosphorylation of ADP to ATP (DT-phosphorylation; e.g. -Omy), the reference rate Z is R in living cells at physiologically controlled steady states of [ADP] and ATP-turnover. The background rate Y is L, and the corresponding flux control efficiency is:
- R-L control efficiency, jR-L = (R-L)/R = 1-L/R.
- 2. If the metabolic control variable is stimulation by ATP turnover or release of an inhibitor of phosphorylation of ADP to ATP (DT-phosphorylation; e.g. -Omy), the reference rate Z is R in living cells at physiologically controlled steady states of [ADP] and ATP-turnover. The background rate Y is L, and the corresponding flux control efficiency is:
- 3. If the background rate Y is L, the metablic control variable from L to R is cell-controlled ATP turnover or release of an inhibitor of phosphorylation of ADP to ATP, and the reference rate Z is E, the coupling control ratio is expressed as the net R/E control ratio (compare 1 and 2):
- (R-L)/E
- 3. If the background rate Y is L, the metablic control variable from L to R is cell-controlled ATP turnover or release of an inhibitor of phosphorylation of ADP to ATP, and the reference rate Z is E, the coupling control ratio is expressed as the net R/E control ratio (compare 1 and 2):
References
Keywords
- Expand Bioblast links to Flux control efficiency
4-compartmental OXPHOS model. (1) ET capacity E of the noncoupled electron transfer system ETS. OXPHOS capacity P is partitioned into (2) the dissipative LEAK component L, and (3) ADP-stimulated P-L net OXPHOS capacity. (4) If P-L is kinetically limited by a low capacity of the phosphorylation system to utilize the protonmotive force pmF, then the apparent E-P excess capacity is available to drive coupled processes other than phosphorylation P» (ADP to ATP) without competing with P».
- Bioblast links: Coupling control - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
1. Mitochondrial and cellular respiratory rates in coupling-control states
| Respiratory rate | Defining relations | Icon | |
|---|---|---|---|
| OXPHOS capacity | P = P´-Rox | mt-preparations | |
| ROUTINE respiration | R = R´-Rox | living cells | |
| ET capacity | E = E´-Rox | » Level flow | |
| » Noncoupled respiration - Uncoupler | |||
| LEAK respiration | L = L´-Rox | » Static head | |
| » LEAK state with ATP | |||
| » LEAK state with oligomycin | |||
| » LEAK state without adenylates | |||
| Residual oxygen consumption Rox | L = L´-Rox |
2. Flux control ratios related to coupling in mt-preparations and living cells
| FCR | Definition | Icon | |
|---|---|---|---|
| L/P coupling-control ratio | L/P | » Respiratory acceptor control ratio, RCR = P/L | |
| L/R coupling-control ratio | L/R | ||
| L/E coupling-control ratio | L/E | » Uncoupling-control ratio, UCR = E/L (ambiguous) | |
| P/E control ratio | P/E | ||
| R/E control ratio | R/E | » Uncoupling-control ratio, UCR = E/L | |
| net P/E control ratio | (P-L)/E | ||
| net R/E control ratio | (R-L)/E |
3. Net, excess, and reserve capacities of respiration
| Respiratory net rate | Definition | Icon |
|---|---|---|
| P-L net OXPHOS capacity | P-L | |
| R-L net ROUTINE capacity | R-L | |
| E-L net ET capacity | E-L | |
| E-P excess capacity | E-P | |
| E-R reserve capacity | E-R |
4. Flux control efficiencies related to coupling-control ratios
| Coupling-control efficiency | Definition | Icon | Canonical term | ||
|---|---|---|---|---|---|
| P-L control efficiency | jP-L | = (P-L)/P | = 1-L/P | P-L OXPHOS-flux control efficiency | |
| R-L control efficiency | jR-L | = (R-L)/R | = 1-L/R | R-L ROUTINE-flux control efficiency | |
| E-L coupling efficiency | jE-L | = (E-L)/E | = 1-L/E | E-L ET-coupling efficiency » Biochemical coupling efficiency | |
| E-P control efficiency | jE-P | = (E-P)/E | = 1-P/E | E-P ET-excess flux control efficiency | |
| E-R control efficiency | jE-R | = (E-R)/E | = 1-R/E | E-R ET-reserve flux control efficiency |
5. General
- » Basal respiration
- » Cell ergometry
- » Dyscoupled respiration
- » Dyscoupling
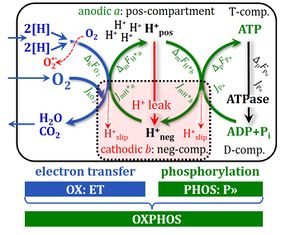
- » Electron leak
- » Electron-transfer-pathway state
- » Hyphenation
- » Oxidative phosphorylation
- » Oxygen flow
- » Oxygen flux
- » Permeabilized cells
- » Phosphorylation system
- » Proton leak
- » Proton slip
- » Respiratory state
- » Uncoupling
- Bioblast links: Normalization - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
- Quantities for normalization
- » Count in contrast to Number
- » Mitochondrial marker
- » O2k-Protocols: mitochondrial and marker-enzymes
- » Citrate synthase activity
- Quantities for normalization
- General
- Related keyword lists
MitoPedia concepts:
MiP concept,
Respiratory control ratio,
SUIT concept
MitoPedia methods:
Respirometry
Labels: MiParea: Respiration
Regulation: Flux control
HRR: Theory